Relasi dan Fungsi Matematika Kelas 8 SMP

Apa itu relasi?

Sobat mungkin sudah tidak asing lagi dengan istilah relasi. Sobat sering menyebutnya sebagai “hubungan”. Untuk lebih jelasnya yuk simak uraian berikut.

Contoh, ada 4 orang anak Eko, Rina, Tono, dan Dika. Mereka diminta untuk menyebutkan warna favorit mereka. Hasilnya adalah sebagai berikut:

Eko menyukai warna merah
Rina menyukai warna hitam
Tono menyukai warna merah
Dika menyukai warna biru

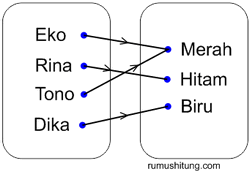
Dari hasil uraian di atas terdapat dua buah himpunan. Pertama adalah himpunan anak, kita sebut dengan A dan himpunan warna yang kita sebut dengan B. Hubungan antara A dan B digambarkan seperti ilustrasi di bawah ini:

Kesimpulannya, relasi antara himpunan A dan himpunan B adalah “suka dengan warna”. Eko dipasangkan dengan merah karena eko suka dengan warna merah. Rina dipasangkan dengan warna hitam karena rina menyukai warna hitam, dan seterusnya. Dari uraian di atas kita dapat mengambil kesimpulan bahwa definisi relasi adalah

“Relasi antara dua himpunan, contoh himpunan A dengan himpunan B adalah suatu aturan yang memasangkan anggota-anggota himpunan A dengan anggota-anggota himpunan B.”

Bagaimana menuliskan sebuah relasi?

Hubungan atau relasi antara dua himpunan dapat dituliskan atau dinyatakan menggunakan tiga buah cara sebagai berikut:

a. Diagram Panah

Perhatikan gambar di bawah ini. Relasi antara himpunan A dengan himpunan B dinyatakan dengan panah-panah yang memasangkan anggota himpunan A dengan anggota himpunan B. Karena penggambarannya menggunakan bentuk panah (arrow) maka disebut dengan diagram panah.

 

b. Himpunan Pasangan Berurutan

Sebuah relasi juga dapat dinyatakan dengan menggunakan pasangan beruturan. Artinya kita memasangkan himpunan A dengan himpunan B secara berurutan.

Eko menyukai warna merah
Rina menyukai warna hitam
Tono menyukai warna merah
Dika menyukai warna biru

Sobat bisa menyatakan relasinya dengan pasangan berurutan sebagai berikut:
(eko,  merah), (rina, hitam),(tono, merah),(dika, biru).

Jadi relasi antara himpunan A dengan himpunan B dapat dinyatakan sebagai pasangan berurutan (x,y) dengan x ∈ A dan y ∈ B.

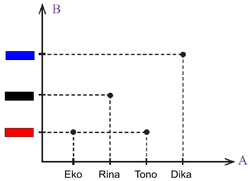
c. Diagram Cartesius

Relasi antara dua himpunan dapat dinyatakan ke dalam pasangan berurutan yang kemudian dituangkan dalam dot (titik-titk) dalam diagram cartesius. Contoh dari relasi suka dengan warna di atas dapat digambarkan dalam bentuk diagram cartesius sebagai berikut:

 

Fungsi

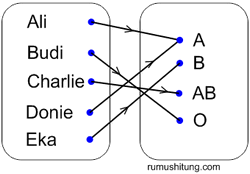
Selain fungsi dikenal juga istilah pemetaan. Keduanya memiliki makna yang sama. Perhatikan ilustrasi di bawah ini:

Dari gambar di atas terdapat dua himpunan yaitu himpunan P ={Ali, Budi, Cahrlie, Donie, Eka} dan himpunan Q ={A,B,O,AB}. Setiap orang dalam himpunan P dipasangkan tepat dengan satu golongan darah yang merupakan anggota himpunan Q. Bentuk relasi yang seperti inilah yang disebut dengan fungsi. Jadi definisi fungsi atau pemetaan adalah

“Fungsi atau pemetaan adalah hubungan atau relasi spesifik yang memasangkat setiap anggota suatu himpunan dengan tepat satu anggota himpunan yang lain.”

Domain, Kodomain, dan Range Fungsi

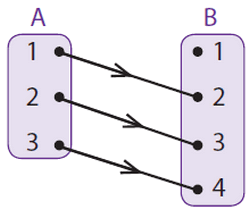
Dalam materi fungsi dikenal istilah Domain, Kodomain, dan juga Range Fungsi. Coba sobat perhatikan gambar di bawah ini.

Dari diagram panah tersebut himpunan A atau himpunan daerah asal disebut dengan Domain. Himpunan B yang merupakan daerah kawan disebut dengan Kodomain sedangkan anggota daerah kawan yang merupakan hasil dari pemetaan disebut dengan daerah hasil atau range fungsi. Jadi dari diagram panah di atas dapat disimpulkan

Domain (Df) adalah A = {1,2,3}
Kodomain adalah B = {1,2,3,4}
Range Hasil (Rf) adalah = {2,3,4}

Grafik Fungsi

Grafi fungsi adalah grafik yang menggambarkan bentuk suatu fungsi dalam diagram cartesius. Grafik ini diperoleh dengan menghubungkan noktah-noktah yang merupakan pasangan berurutan antara daerah asal (sumbu x) dan daerah hasil (sumbu y).

Menghitung Nilai dari Sebuah Fungsi

1. Notasi Fungsi

Sebuah fungsi dinotasikan dengan huruf kecil seperti f, g, h, i, dan sebagainya. Pada fungsi g yang memetakan himpunan A ke himpunan B dinotasikan dengan g(x). Misal ada fungsi f yang memetakan A ke B dengan aturan f : x → 2x + 2. Dari notasi fungsi tersebut, x merupakan anggota domain. fungsi x → 2x + 2 berarit fungsi f memetakan x ke 2x+2. Jadi daerah bayangan x oleh fungsi f adalah 2x + 2. Sobat dapat menotasikannya dengan f(x) = 2x +2. Kesimpulan

Jika fungsi f : x → ax + b dengan x anggota domain f maka rumus fungsi f adalah f(x) = ax +b

2. Menghitung nilai dari Sebuah Fungsi

Menghitung nilai dari sebuah fungsi cukup sederhana. Sobat hanya perlu mengikuti rules dari fungsi tersebut. Semakin susah fungsi yang memetakannya maka akan semakin susah menghitung nilai fungsinya. Terkadang soal-soal membalik fungsi tersebut, diketahui daerah hasil kemudian diminta mencari daerah asal. Yuk mari dismak contoh berikut:

Diketahui fungsi f : x → 2x – 2 dengan x anggota bilangan bulat. Coba sobat tentukan nilai dari

1. f(3)
2. f(4)
3. bayangan (-3) oleh f
4. nilai f untuk x = -10
5. nilai a jika f(a) = 14

Jawaban
fungsi fungsi f : x → 2x – 2 dapat dinyatakan dengan f(x) = 2x – 2

1. f(x) = 2x – 2
   f(1) = 2(3) – 2 = 4
2. f(x) = 2x – 2
   f (4) = 2(4) – 2 = 6
3. f(x) = 2x – 2
   f(-3) = 2(-3) – 2 = -8
4. f(x) = 2x – 2
   f(10) = 2(10) -2 = 18
5. f(a) = 2a – 2
   14 = 2a -2
   2a = 16
   a = 8

3. Menentukan Rumus sebuah fungsi

Sebuah fungsi dapat sobat temukan rumusnya apabila ada nilai atau data yang diketehui. Kemudian dengan menggunakan aljabar sobat bisa dengan mudah menemukan rumus dari fungsi tersebut. Untuk lebih jelasnya bisa sobat simak contoh berikut:

Fungsi g yang berlaku pada himpunan bilangan riil ditentukan oleh rumus g(x) = ax + b dengan a dan b adalah bilangan bulat. Jika g(-2) = -4 dan g(1) = 5. Coba sobat tentukan nalai dari:

1. nilai dari a dan b
2. rumus fungsi
3. g (-3)

Jawaban

1. Untuk mencari nila a dan b kita buat persamaan dulu dari himpunan pasangan berurutan yang diketahui.
   g(-2) = -4 → -4 = -2a + b → b = 2a – 4 …(1)
   g(1) = 5    →  5 = a + b …(2)
   kita substitusikan persamaan 1 ke persamaan 2

   5 5 5 9 a

   = a + b = a + 2a – 4 = 3a – 4 = 3a = 3

   b = 2a – 4
   b = 2(3) -4
   b = 2
   jadi nilai a = 3 dan b = 4
2. rumus fungsinya g(x) = 3a + 2
3. g(x) = 3a + 2
   g(-3) = 3 (-3) + 2
   g (-3) = -7

 Demikian sobat materi dari kami tentang relasi dan fungsi matematika kelas 8 SMP. Semoga bisa membantu belajar kalian di rumah

pecahan operasi aljabar

Operasi – Operasi Pecahan Bentuk Aljabar

• Penjumlahan Dan Pengurangan Bentuk Aljabar

Ketika berada dikelas VII temen-temen telah mempelajari bersama operasi penjumlahan dan pengurangan pada pecahan aljabar dengan penyebut suku satu. Sama seperti pada kasus penjumlahan dan pengurangan penyebut suku satu, pada pecahan bentuk aljabar dengan penyebut suku dua serta sama dapat langsung dijumlahkan atau dikurangkan pembilangnya.
Dimana pada penjumlahan dan pengurangan pecahan aljabar dengan penyebut yang berbeda dapat dilakukan dengan cara menyamakan penyebutnya menjadi sebuah kelipatan persekutuan terkecil (KPK) dari penyebut-penyebutnya.
adversitemens

Jadi aljabar dengan penyebut suku dua pada prinsipnya sama dengan suku satu, kita tinggal samakan penyebutnyaa, baru kita jumlahkan atau kalikan pembilangnyaa. Agar semakin paham, perhatikan contoh berikut.

Jadi setelah memperhatikan contoh diatas semakin paham cara menyelesaikan penjumlahan dan pengurahan pecahan bentuk aljabar dua suku kan yaa sekarang. Karena prinsipnya sama seperti pecahahn sederhana.

• Perkalian Dan Pembagian Pecahan Aljabar

Ketika kita akan mengalikan dua buah pecahan kita dapat melakukannya dengan mengalikan antara pembilang dengan pembilang serta penyebut dengan penyebut.

Untuk lebih memahami perkalian pecahan bentuk aljabar, perhatikan contoh berikut.

Jadi mudah bukan cara menyelesaikan perkalian pecahan bentuk aljabar, karena pada prinsipnya sama seperti perkalian biasa, bagian penyebut kita kalian dengan penyebut begitu juga bagian pembilang kita kalikan dengan pembilang juga. Semakin paham kan yaa sekarang….

Selanjutnya untuk pembagian pecahan bentuk aljabar dikerjakan dengan mengubah bentuk pembagian tersebut menjadi bentuk perkalian dengan cara mengalikan dengan kebalikan pecahan pembagi.

agar lebih paham mengenai konsep pembagian pecahan bentuk aljabar perhatikan contoh berikut.

Jadi untuk pembagian sama aja kita mengerjakan bentuk perkalian, karena pembagian akan diubah kedalam bentuk perkalian. Jika temen-temen sudah sangat paham mengerjakan bentuk perkalian maka akan sangat mudah juga mengerjakan bentuk pembagian karena prinsipnya sama.

• Menyederhanakan Pecahan Aljabar

Sebuah bentuk pecahan dikatakan sederhana jika pembilang serta penyebutnya tidak lagi memiliki faktor persekutuan, kecuali 1. Dengan perkataan lain, jika sebuah pembilang serta penyebut sebuah pecahan memilki faktor yang sama kecuali satu maka pecahan tersebut dapat disederhanakan. Dimana perihal seperti ini juga berlaku pada pecahan bentuk aljabar.

Dalam menyederhakan pecahan bentuk aljabar dapat kita lakukan dengan memfaktorkan pembilang serta penyebutnya terlebih dahulu, selanjutnya dibagi dengan faktor sekutu dari pembilang dan penyebut tersebut. Agar lebih paham tentang menyederhanakan pecahan bentuk aljabar, perhatikan contoh berikut.

Setelah memperhatikan contoh diatas temen-temen sudah semakin paham kan ya, bagaimana cara menyederhanakan pecahan bentuk aljabar. Sangat mudah bukan? kita tinggal memfaktorkan lalu kita hilangkan persekutuannya.

• Menyederhanakan Pecahan Bersusun

Sebuah pecahan bersusun atau kompleks merupakan suatu pecahan yang pembilang serta penyebutnya ataupun kedua-duanya masih memuat pecahan. Untuk menyederhakan bentuk pecahan bersusun seperti ini, kita dapat melakukannya dengan cara mengalikan pembilang dan penyebutnya dengan KPK dari penyebut pecahan pada pembilang dan penyebut pecahan pada penyebut bersusun itu. Perhatikan secara seksama contoh berikut agar temen-temen lebih mudah memahami cara menyederhakan pecahan bersusun.

  

Faktor Faktor suku Aljabar

Faktor Bentuk Aljabar

Kalian masih ingat dengan istilah faktor suku aljabar? Bentuk aljabar xy merupakan perkalian dari x dengan y (xy = x × y). Maka yang menjadi faktor dari xy adalah x dan y. Begitu juga dengan bentuk a(x + y), dimana faktor dari a(x + y) adalah a dan (x + y).

Jadi, yang dimaksud dengan pemfaktoran bentuk aljabar adalah menyatakan bentuk penjumlahan suku-suku ke dalam bentuk perkalian atau faktor.

1. Hukum Distributif dan Faktor Persekutuan Aljabar

1. Hukum Distributif dan Faktor Persekutuan Aljabar

Masih ingat dengan hukum distributif untuk bilangan a, b, c anggota bilangan real? pada hukum distributif berlaku aturan

Untuk memfaktorkan bentuk aljabar dapat menggunakan hukum distributif. Langkah pertama yang harus dilakukan adalah mencari faktor persekutuan terbesar dari setiap suku aljabar.

Perhatikan contoh berikut.

Faktorkanlah bentuk aljabar berikut ini!
a. 2x2 + 8x2y
b. 12abc + 15xyz
c. 3x2y – 15xy2z

Penyelesaian:

a. 2x2 + 8x2y = 2x2 (1 + 4y) (FPB 2x2 dan 8x2y = 2x2)

b. 12abc + 15xyz = 3(4abc + 5xyz) (FPB 12abc dan 15xyz = 3)

c. 3x2y – 15xy2z = 3xy(x - 5yz) (FPB 3x2y dan 15xy2z = 3xy)

2 Faktorisasi Bentuk x2 + 2xy + y2

Ayo kita tinjau kembali hasil perkalian bentuk (x + y)2. Hasil perkalian dari (x + y)2 adalah x2 + 2xy + y2. Bentuk seperti ini disebut sebagai bentuk kuadrat sempurna.

Bentuk kuadrat sempurna mempunyai beberapa ciri khusus, yaitu:
a. Koefisien peubah pangkat dua (x2) sama dengan 1.
b. Konstanta merupakan hasil kuadrat setengah koefisien x.

Perhatikan contoh berikut ini!

Faktorkanlah bentuk kuadrat sempurna dari x2 + 8x + 16!

Penyelesaian:

Konstanta = (½ × 8)2 = 42, maka
x2 + 8x + 16 = x2 + 8x + (4)2
                     = (x + 4)2
                     = (x + 4)(x + 4)

Selain dengan cara di atas, memfaktorkan bentuk kuadrat sempurna dapat diselesaikan dengan hukum distributif. Caranya adalah mengubah suku 2xy menjadi penjumlahan dua suku (xy + xy), kemudian suku-suku tersebut difaktorkan.

Perhatikan contoh berikut ini!

Faktorkanlah bentuk kuadrat sempurna dari x2 + 8x + 16!

Penyelesaian:
x2 + 8x + 16 = x2 + 4x + 4x + 16

 = (x2 + 4x) + (4x + 16)
                     = x (x + 4) + 4(x + 4)
                     = (x + 4) (x + 4)
                     = (x + 4)2
Jadi faktor dari x2 + 4x + 16 adalah (x + 4)2

3. Faktorisasi Bentuk Kuadrat ax2 + bx + c

Selain faktorisasi bentuk x2 + 2xy + y2, faktorisasi bentuk kuadrat terdapat pula dalam bentuk ax2 + bx + c; dengan a, b, dan c merupakan bilangan real. a dan b merupakan koefisien, c adalah konstanta. Sedangkan yang menjadi peubah atau variabel adalah x2 dan x.

a. Memfaktorkan bentuk ax2 + bx + c, jika a = 1

Untuk memfaktorkan bentuk aljabar seperti ini, kalian harus memperhatikan bentuk perkalian suku (x + y) dengan (x + z) berikut.
(x + y)(x + z) = x(x + z) + y(x + z) (sifat distributif)
                      = ((x.x)+(x.z))+((y.x)+(y.z)) (sifat distributif)
                      = x2 + xz + xy + yz
                      = x2 + (y + z)x + yz

Perhatikan contoh berikut ini!

Faktorkanlah bentuk aljabar dari x2 + 7x + 12!

Penyelesaian:
x2 + 7x + 12 = x2 + (y + z)x + yz
y + z = 7
yz = 12
y dan z yang memenuhi adalah y = 3 dan z = 4 atau y = 4 dan z = 3.

Jadi bentuk kuadrat dari x2 + 7x + 12 adalah:
(x+y)(x+z) = (x + 3)(x + 4)
atau
(x+y)(x+z) = (x + 4)(x + 3).

b. Memfaktorkan bentuk ax2 + bx + c, jika a ¹ 1

Kalian telah memahami bahwa pemfaktoran bentuk ax2 + bx + c, jika a = 1 adalah (x + y)(x + z). Dengan menurunkan rumus tersebut kita dapat memperoleh rumus pemfaktoran ax2 + bx + c untuk a ≠ 1. Perhatikan pemfaktoran berikut!

Selanjutnya kita cari bilangan yang jika dijumlahkan hasilnya sama dengan b/a dan jika dikalikan hasilnya sama dengan b/c.

Faktorkanlah bentuk aljabar 2x2 + 3x – 14!

Penyelesaian:

2x2 + 3x – 14 = a(x+ p/a )( x+ q/a)
Berdasarkan soal, diperoleh nilai a = 2, b = 3, dan c = –14, sehingga:
pq = ac = –28
p + q = b = 3
Nilai p dan q yang memenuhi adalah p = –4 dan q = 7, atau p = 7 dan q = –4.

Jadi,
Untuk p = –4 dan q = 7
2x2 + 3x – 14 = 2(x + –4/2 )( x + 7/2 )
                      = (x - 2)(2x + 7)

Untuk p = 7 dan q = -4
2x2 + 3x – 14 = 2( x + 7/2 )(x + -4/2 )
                      = (2x + 7)(x - 2)

Jadi faktor dari 2x2 + 3x – 14 adalah (2x + 7)(x - 2)